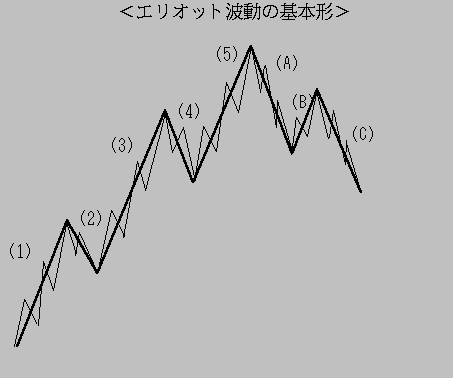

丂僄儕僆僢僩攇摦偼丄忋徃憡応偵偍偄偰偼丄忋徃俆攇丄壓崀俁攇偺寁俉攇偑婎杮偺宍
偱偁傞丅(忋恾嶲徠)
忋徃俆攇偼丄俁偮偺悇恑攇偲俀偮偺挷惍攇偐傜側傝丄壓崀俁攇偼丄俀偮偺悇恑攇偲
侾偮偺挷惍攇偐傜側偭偰偄傞丅悇恑攇偲偼丄戝偒側攇偲摨偠曽岦偵摦偔攇摦偱丄
挷惍攇偲偼丄戝偒側攇偲媡偺曽岦偵摦偔攇摦偱丄忋恾偱乮侾乯乮俁乯乮俆乯偑悇恑攇
丄乮俀乯乮係乯偑挷惍攇偱偁傞丅
丂偦傟偧傟偺攇摦偼丄偝傜偵摨條偺攇摦偵嵶暘壔偝傟傞丅乮侾乯乮俁乯乮俆乯
乮俙乯乮俠乯偼丄俆攇摦偵丄乮俀乯乮係乯乮俛乯偼丄俁攇摦偵傢偐傟傞丅
乮侾乯偺攇摦偑丄嘆 嘇 嘊 嘋 嘍偵傢偐傟傞偲偡傞偲丄嘆丂 嘊丂丂嘍偼丄
偝傜偵俆攇摦偵丄嘇丂嘋偼丄偝傜偵俁攇摦偵傢偐傟傞丅
丂偄偪偽傫傕偲偺宍偼丄忋徃偺俆攇摦丄壓崀偺俁攇摦偱慡晹偱俉攇摦丅偙偺俁丄俆丄
俉偲偄偆悢帤慡偰偑僼傿儃僫僢僠悢偱偁傞丅師偺嵶暘壔偱偼丄忋徃俀侾攇摦丄
壓崀侾俁攇摦偱慡晹偱俁係攇摦丅偙偺侾俁丄俀侾丄俁係傕僼傿儃僫僢僠悢偱偁傞丅
偝傜側傞嵶暘壔偱偼丄忋徃俉俋攇摦丄壓崀俆俆攇摦偱慡晹偱侾係係攇摦丅偙偺
俆俆丄俉俋丄侾係係傕僼傿儃僫僢僠悢偱偁傞丅
丂僼傿儃僫僢僠悢偵偮偄偰偼丄偁偲偱偔傢偟偔愢柧偡傞梊掕偱偁傞丅
丂[僄僋僗僥儞僔儑儞]
丂摨偠丄悇恑攇偱傕丄戞侾攇丄戞俁攇丄戞俆攇偱偼丄偨偄偰偄戝偒偝偼堎側傞丅
戞侾攇丄戞俁攇丄戞俆攇偺偆偪偺偄偢傟偐偑偝傜偵俆偮偺彫偝側攇偵暘偐傟偰戝偒偔
側傞応崌丄偄傢備傞僄僋僗僥儞僔儑儞乮奼挘乯傪帵偡帪偑偁傞丅
晛捠丄戞侾攇偼丄戝掙偐傜偺夞暅夁掱偱丄偦傟傎偳丄戝偒側忋徃偵偼側傜側偄偙偲偑
懡偄丅戝偒偔側傞偺偼丄戞俁攇丄傑偨偼丄戞俆攇偺偙偲偑懡偄丅壓恾傪嶲徠偟偰
偄偨偩偒偨偄丅
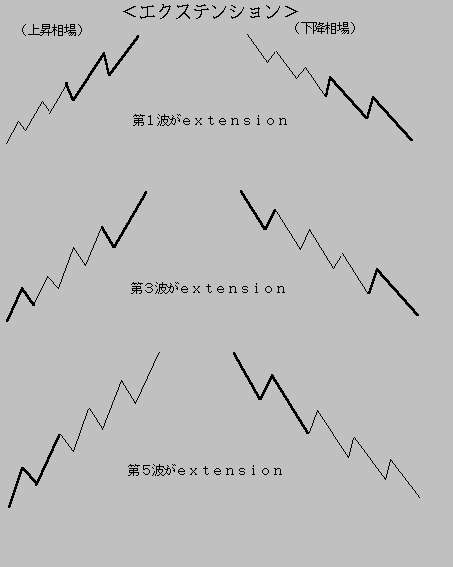
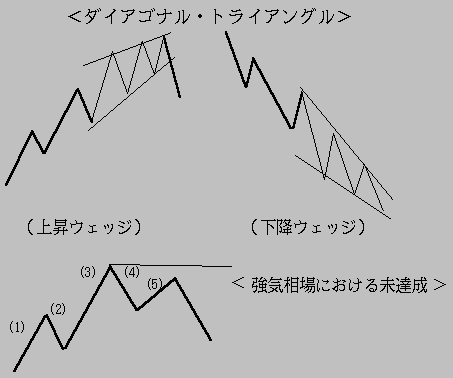
[僟僀傾僑僫儖丒僩儔僀傾儞僌儖]
僟僀傾僑僫儖丒僩儔僀傾儞僌儖偼丄幬傔嶰妏宍偱丄捠忢嵟廔攇摦偺戞俆攇偵尰傟傞 丅偙偺僟僀傾僑僫儖丒僩儔僀傾儞僌儖傪峔惉偡傞攇摦偼丄戞侾攇丄戞俁攇丄戞俆攇 偺弴偺戝偒偝偱丄師戞偵彫偝偔幭媗傑偭偰丄戝偒側攇摦偑廔椆偡傞丅
[枹払惉]
捠忢偼丄戞俆攇偼丄戞俁攇偺捀忋傪挻偊傞偑丄偨傑偵丄挻偊偢偵丄枹払惉偱廔傢傞 働乕僗偑偁傞丅偙傟傪丄枹払惉乮僼僃僀儔乕乯偲偄偆丅
丂忋徃攇偱偺乮俀乯乮係乯丄壓崀攇偱偺乮俛乯偑偄傢備傞挷惍攇偱偁傞偑丄偙偺 挷惍攇偵偼丄偄偔偮偐偺僷僞乕儞偑偁傞丅
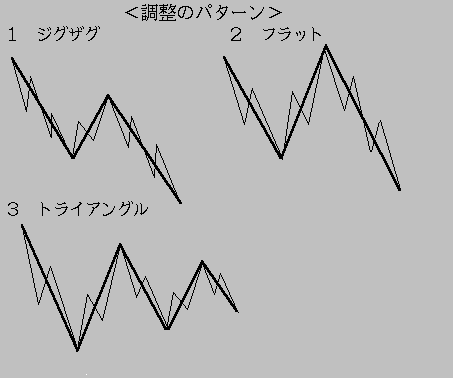
丂[僕僌僓僌]
丂丂捠忢丄傕偭偲傕懡偔尒傜傟傞僷僞乕儞丅俙亅俛亅俠偺攇摦偱 丂丂俙偲俠偑俆攇摦偱丄俛偑俁攇摦偺俆乕俁乕俆偺僷僞乕儞丅俛攇偼丄俙攇偺揤堜 偵偼媦偽側偄丅偙偺僕僌僓僌偺曄宍偱丄俙亅俛亅俠亅倃亅俙乫亅俛乫亅俠乫偺 丂丂僟僽儖丒僕僌僓僌偑丄戝偒側挷惍偺帪偵偨傑偵尒傜傟傞丅
丂[僼儔僢僩]
嫮偄抧崌偄偺帪偵椙偔尒傜傟傞丅俙偲俛偑俁攇摦偱丄俠偑俆攇摦偺俁乕俁乕俆偺 僷僞乕儞丅俛攇偼丄俙攇偺揤堜傪挻偊丄俠攇偼丄俙攇偺掙傪壓夞傞偙偲偑懡偄丅 丂 俛攇偼丄媫寖側栠偟偵側傞偙偲偑懡偄丅僼儔僢僩偺曄宍偵儔儞僯儞僌挷惍偑偁傞 丂 丅俛偑俙攇偺揤堜傪挻偊丄側偍偐偮俠攇偑俙攇偺掙傪忋夞傞宍丅
丂 丂[僩儔僀傾儞僌儖]
戞係攇偱椙偔尒傜傟傞僷僞乕儞丅嶰妏帩偪崌偄偲傕偄傢傟傞丅戝偒側攇摦偐傜
丂 師戞偵彫偝側攇摦偵側傝丄幭媗傑偭偨屻偵丄儊僀儞丒僩儗儞僪傊曻傟偰偄偔丅
丂 僩儔僀傾儞僌儖偼丄晛捠丄俆攇摦偱峔惉偝傟丄偦傟偧傟偺攇摦偼丄俁攇摦偵
丂 暘偐傟傞丅
丂丂 僩儔僀傾儞僌儖偼丄宍偱丄傾僙儞僨傿儞僌丒僩儔僀傾儞僌儖乮忋曽傊偺
丂 嶰妏宍乯丄僔儞儊僩儕僇儖丒僩儔僀傾儞僌儖乮忋壓懳徧乯丄僨傿僙儞僨傿儞僌丒
丂 僩儔僀傾儞僌儖乮壓曽傊偺嶰妏宍乯偵暘偗傜傟傞丅
丂偙偺挷惍攇偵偮偄偰偼丄僆乕僞僱乕僔儑儞乮岎懼乯偺朄懃偑揔梡偝傟丄戞俀攇偲 戞係攇偺挷惍僷僞乕儞偑摨偠傕偺偵側傞偙偲偼側偄丅偨偲偊偽丄戞俀攇偱丄扨弮側 僕僌僓僌挷惍偱偁傟偽丄戞係攇偼丄僕僌僓僌埲奜偺僼儔僢僩挷惍傗僩儔僀傾儞僌儖 偵側傞偱偁傠偆丅媡偵丄戞俀攇偑丄僼儔僢僩偱偁傟偽丄戞係攇偼丄僕僌僓僌偵側傞 壜擻惈偑崅偄偲偄偊傛偆丅
丂 僼傿儃僫僢僠悢丄偙偺恄旈偺悢楍傪敪尒偟偨偺偼丄侾俁悽婭偺悢妛幰丄儗僆僫儖僪丒 僼傿儃僫僢僠偱偁傞丅
丂侾亄侾亖俀丂侾亄俀亖俁丂俀亄俁亖俆丂俁亄俆亖俉丂俆亄俉亖侾俁 偙偺傛偆偵丄楢懕偡傞俀偮偺悢傪懌偟偨傕偺偑丄師偺悢偵側傞丅
侾丄侾丄俀丄俁丄俆丄俉丄侾俁丄俀侾丄俁係丄俆俆丄俉俋丄侾係係丄俀俁俁
丂[偙偺悢楍偺嬌傔偰嫽枴怺偄揰]
丂偁傞悢傪侾偮慜偺悢偱妱傞偲丄侾丏俇侾俉丅侾偮屻傠偺悢偱妱傞偲丂侽丏俇侾俉丅 丂 丂俆俆亐俁係亖侾丏俇侾俈俇丂丂丂俆俆亐俉俋亖侽丏俇侾俈俋 丂 丂侾丏俇侾俉倃侽丏俇侾俉亖侾
丂偁傞悢傪俀偮慜偺悢偱妱傞偲丂俀丏俇侾俉丅俀偮屻傠偺悢偱妱傞偲丂侽丏俁俉俀丅 丂 丂侾係係亐俆俆亖俀丏俇侾俉侾丂丂俁係亐俉俋亖侽丏俁俉俀侽丂 丂 丂俀丏俇侾俉倃侽丏俁俉俀亖侾 丂愭傎偳偺侽丏俇侾俉傪擇忔偡傞偲侽丏俁俉俀丅侾丏俇侾俉傪擇忔偡傞偲俀丏俇侾俉 丂偵側傞丅
丂丂偙偺侽丏俁俉俀傗侽丏俇俉俀丄侾丏俇侾俉傗俀丏俇侾俉偼僄儕僆僢僩攇摦偱偺
丂栚昗抣傪掕傔傞偺偵寚偐偣側偄悢帤偱偁傞丅
丂丂崅抣傑偨偼埨抣偐傜偺墴偟傗栠傝傪梊憐偡傞応崌丆忋徃傑偨偼壓棊偟偨暆偺
丂侽丏俁俉俀攞偐傜侽丏俇侾俉攞偑儊僪偲側傞丅
丂
丂僄儕僆僢僩攇摦偵偮偄偰偼丄偄偔偮偐偺朄懃偑偁傞偑丄偙偙偱偼偦偺拞偱嵟廳梫 偺朄懃偺傒敳悎偡傞丅
丂乭戞俁攇偑丄嵟抁偵側傞偙偲偼側偄丅乭
丂悇恑攇偺戞侾攇丄戞俁攇丄戞俆攇偺拞偱丂戞俁攇偼丂堦斣僄僋僗僥儞僔儑儞偟
傗偡偄攇摦偩偑丄偙偺俁偮偺拞偱丄堦斣抁偔側傞偙偲偼側偄偺偱偁傞丅戞俁攇偑
堦斣抁偔側傞傛偆側攇摦偺庢傝曽偼丄娫堘偭偰偄傞偺偱偁傞丅
丂傕偟丂戞俁攇偑戞侾攇傛傝傕抁偐偭偨応崌丄戞俆攇偼摉慠偺偙偲側偑傜戞俁攇
傛傝傕抁偔側傞丅偲偄偆偙偲偼丄戞俆攇偺揤堜偺嵟崅抣丄傑偨偼掙偺嵟埨抣偼丄梊憐
偑偁傞掱搙偮偔偙偲偵側傞丅
丂 丂偙傟偩偗傪婥傪偮偗傟偽丄僄儕僆僢僩攇摦偺廗摼偵偼丄栤戣側偄偼偢偱偁傞丅